Recursion on Nested Lists and Expressions

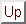
So far we have worked only with simple lists. These are lists for which the top-level elements are our only concern. For example, given the list '(1 a (5 g) up), the top-level elements are: 1, a, (5 g), and up. But often we are interested in looking deeper than just the top-level. A nested list consists of atoms and lists; the latter may themselves be nested. Searching, deleting, inserting, replacing atoms in a multi-level list, or evaluating arbitrarily complex mathematical expressions are all naturally recursive problems on nested lists. Such recursion is slightly more complicated than recursion on simple lists, but it again follows a common, general structure.

 
RULE OF THUMB 3:

   When recurring on a nested list, do three things:

      1. check for the termination condition;

      2. check if the first element of the list is an atom or a list;

      3. recur with the ``first'' and the ``rest'' of the list.

 
Example 3:

  Write a function, ``search,'' which takes a nested list and an atom, and

  it returns  't if it finds the atom within the nested list and returns  nil

  otherwise.

To write this function, let's take the steps recommended by Rule of Thumb 3:

(1)

We will move through the list one element at a time and if we reach the end without finding the given atom, we will return (). To check for termination we can use the predicate ``null.''

(2)

At each step we will look at the first element of the list; if it is an atom we will check if it equals the given atom. If they match, we can return 't immediately, else we go on with the search in the rest of the list. We can use the predicate ``atom'' to check if the first element is an atom. We can use ``equal'' to test for equality.

(3)

Lastly, if we discover that the first element is a list, we may need to perform two searches: the first within the nested list represented by the first element; the second within the ``rest'' of the original list. If the result of either of these searches is 't, the overall result is also true. We can use the logical function ``or'' to get this effect.

          (defun search (lst elt)
             (cond ((null lst) nil)
                   ((atom (first lst))
                    (if (equal (first lst) elt)
                        't
                        (search (rest lst) elt)))
                   (t (or (search (first lst) elt)
                          (search (rest lst) elt)))))

(search '(a (1 c) 2 7) 'c)
        = (search '((1 c) 2 7) 'c)
        = (or (search '(1 c) 'c) (search '(2 7) 'c))
        = (or (search '(c) 'c) (search '(2 7) 'c))
        = (or 't (search '(2 7) 'c))
        = 't

 
RULE OF THUMB 4:

   When evaluating an expression, do three things:

      1. check for the termination condition;

      2. identify operator;

      3. apply operator to recursive calls on the operands.

 
Example 4:

  Write a function, ``evaluate,'' which takes a prefix expression represented

  as a nested list and returns the numerical value represented by the

  expression.  Only +, -, and * may be used as operators and each operator

  can have only two operands.  Thus,  (evaluate '(* (+ 4 6) 4)) should

  return 40.

(1)

Note that we are no longer working with a list of elements. The argument of ``evaluate'' represents an expression. If this argument is a list we know that it will have three parts: an operator, the first operand sub-expression, the second operand sub-expression. In this case, we will need to further evaluate the operands. If the argument is a number, we can stop. We can use the predicate ``numberp'' to test for a numerical value.

(2)

We can identify the first element of the argument list as the operator. For each operator we will need to apply a different function.

(3)

For each possible operator we will recursively call evaluate on the first and second operands.

        (defun evaluate (expr)
           (cond ((numberp expr) expr)
                 ((equal (first expr) '+)
                  (+ (evaluate (second expr))
                     (evaluate (third expr))))
                 ((equal (first expr) '-)
                  (- (evaluate (second expr))
                     (evaluate (third expr))))
                 (t
                  (* (evaluate (second expr))
                     (evaluate (third expr))))))

(evaluate '(* (+ 6 3) (- (+ -1 2) 3)))
        = (* (evaluate '(+ 6 3)) (evaluate '(- (+ -1 2) 3)))
        = (* (+ (evaluate 6) (evaluate 3)) 
             (evaluate '(- (+ -1 2) 3)))
        = (* (+ 6 (evaluate 3)) (evaluate '(- (+ -1 2) 3)))
        = (* (+ 6 3) (evaluate '(- (+ -1 2) 3)))
        = (* 9 (evaluate '(- (+ -1 2) 3)))
        = (* 9 (- (evaluate '(+ -1 2)) (evaluate 3)))
        = (* 9 (- (+ (evaluate -1) (evaluate 2)) 
                  (evaluate 3)))
        = (* 9 (- (+ -1 (evaluate 2)) (evaluate 3)))
        = (* 9 (- (+ -1 2) (evaluate 3)))
        = (* 9 (- 1 (evaluate 3)))
        = (* 9 (- 1 3))
        = (* 9 -2)
        = -18